Ada tiga metode yang sering digunakan dalam menyelesaikan persamaan kuadrat, yaitu pemfaktoran, melengkapkan kuadrat sempurna, dan menggunakan rumus abc (rumus kuadrat). Dalam mencari penyelesaian persamaan kuadrat, biasanya kita mencoba memfaktorkannya terlebih dahulu. Jika kita menemui kendala, barulah kita menggunakan rumus abc atau melengkapkan kuadrat sempurna. Kali ini kita akan membuktikan rumus abc dengan cara lain, meskipun prinsipnya sama, yaitu mengubah ruas kiri menjadi bentuk kuadrat sempurna.
Agar ruas kiri bisa diubah menjadi bentuk kuadrat, koefisien dari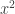 
haruslah bentuk kuadrat. Sebelumnya kita membagi persamaan dengan a, sehingga kita memperoleh koefisien 1 yang merupakan bilangan kuadrat paling sederhana. Dalam pembuktian kali ini, kita mengalikan persamaan dengan 4a, sehingga diperoleh 
sebagai koefisien .
haruslah bentuk kuadrat. Sebelumnya kita membagi persamaan dengan a, sehingga kita memperoleh koefisien 1 yang merupakan bilangan kuadrat paling sederhana. Dalam pembuktian kali ini, kita mengalikan persamaan dengan 4a, sehingga diperoleh sebagai koefisien .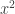
Kurangi kedua ruas dengan 4ac, sehingga.
Tambahkan 
pada kedua ruas.
pada kedua ruas.
Ubah ruas kiri menjadi bentuk kuadrat sempurna.
Tarik akar pada kedua ruas.
Kurangi kedua ruas dengan b.
Bagi kedua ruas dengan 2a.
Terbukti.
